En uno de los segmentos del episodio especial de Noche de Brujas de Los Simpson de 1995, Homero atraviesa un portal en la pared de la sala de su casa rumbo a la tercera dimensión. El universo tridimensional se muestra como un reticulado que a Homero le recuerda a la película "Tron", con figuras geométricas y fórmulas matemáticas. Entre ellas aparece la siguiente igualdad: 1782¹² + 1841¹² = 1922¹²

El último teorema de Fermat
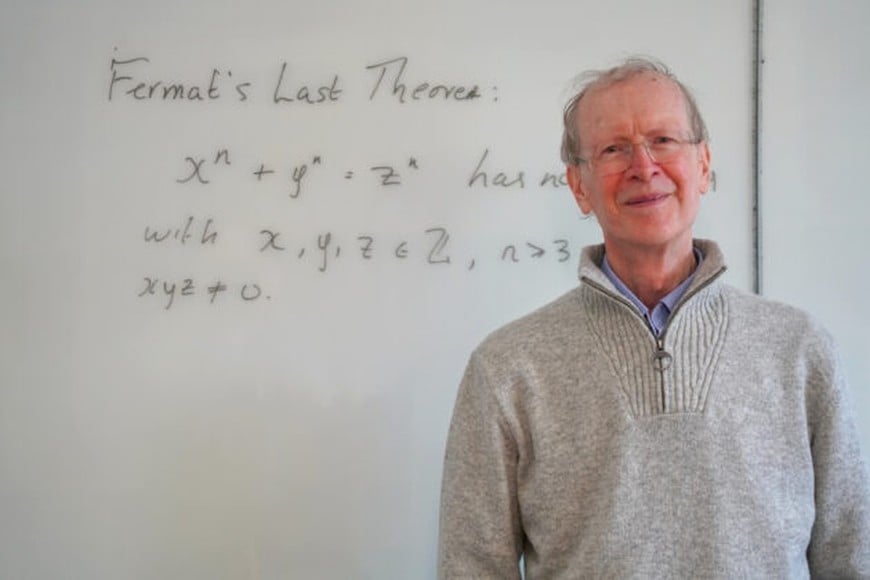
Hay aquí un número elevado a la potencia doce (es decir, multiplicado por sí mismo doce veces), más otro número elevado a la potencia doce, igual a un tercer número, también elevado a la potencia doce. Esta igualdad no debería existir porque viola el llamado Último Teorema de Fermat, un teorema que tiene cierta fama porque fue enunciado en 1670 y fue demostrado en 1995. Hubo que esperar más de trescientos años para que los matemáticos confirmaran algo que este señor Fermat había propuesto en el siglo XVII.
Pierre de Fermat nació en Francia en 1607. Fue abogado, juez y jurista. Además de trabajar en la administración pública, Fermat era matemático aficionado y alrededor de 1640, en un libro del matemático griego Diofanto, tropezó con el concepto de terna pitagórica. Se trata de conjuntos de tres números tales que el cuadrado del primero, más el cuadrado del segundo, es igual al cuadrado del tercero. Por ejemplo, tres al cuadrado (9) más cuatro al cuadrado (16) es igual a cinco al cuadrado (25). Se llaman ternas pitagóricas porque se relacionan con el teorema de Pitágoras.
Fermat se preguntó si el concepto de terna pitagórica podía extenderse a potencias de grado mayor. Si había, por ejemplo, tres números tales que el cubo del primero, más el cubo del segundo, fuera igual al cubo del tercero. Fermat aseguró que no. Que las ternas pitagóricas solamente funcionan con números elevados al cuadrado. No funcionan con números elevados al cubo, a la cuarta potencia, a la quinta potencia ni, en general, con ninguna potencia mayor que dos. Y, ciertamente, no deberían funcionar con potencias de grado doce.
La igualdad aparecida en Los Simpson no contradice realmente la afirmación de Fermat porque tiene un pequeño error de alrededor del 0,00000001%. Eso es tan poco que, si hiciéramos las cuentas en una calculadora común, la daríamos por buena, porque el error es menor a lo que la calculadora podría detectar. Este supuesto contraejemplo del teorema de Fermat fue generado por un programa creado por David Cohen, doctor en computación por la universidad de Berkeley y uno de los productores y guionistas históricos de Los Simpson.
En cualquier caso, Fermat anotó en el margen del libro su observación sobre la inexistencia de ternas pitagóricas de grado mayor que dos. Y agregó: "Tengo una demostración verdaderamente maravillosa de esta proposición pero este margen es demasiado estrecho para contenerla". Fermat murió en 1665. En 1670, su hijo Clement publicó los papeles de su padre, incluyendo su observación sobre las ternas pitagóricas. Pero la "maravillosa demostración" nunca fue encontrada y la afirmación de Fermat se convirtió en el problema no resuelto más famoso de la matemática.
Desde ese momento los matemáticos más importantes del mundo atacaron el teorema con el objetivo de demostrarlo o, en todo caso, de refutarlo. En 1816, la Academia de Ciencias de París ofreció una medalla de oro y un premio en efectivo para el que lograra demostrarlo. Lo mismo hizo la Universidad de Gottinga a principios del siglo XX. Karl Gauss, llamado "El príncipe de la matemática", lo demostró para el caso de cubos. En la década de 1850 el matemático francés André- Marie Legendre demostró que el teorema de Fermat era válido para todas las potencias menores que cien. Ya en el siglo XX se logró probar el teorema para el caso de potencias de hasta grado 125.000. Pero demostrar el teorema implicaba probarlo para todas las potencias posibles.
En 1963 un niño inglés de 10 años, llamado Andrew Wiles (Cambridge, 11 de abril de 1953), encontró en la biblioteca pública de su barrio el libro "El último problema", del matemático y divulgador escocés Eric Temple Bell. El libro contaba la historia del teorema de Fermat desde su origen en la antigua Grecia y las ternas pitagóricas hasta los intentos por resolverlo a lo largo de tres siglos. A Wiles le interesó la historia y el teorema de Fermat se convirtió en su obsesión. Decidió que algún día él demostraría el teorema.
Treinta años después, en junio de 1993, Wiles ofreció una serie de conferencias en el Instituto Newton de la Universidad de Cambridge, Inglaterra. Luego de llenar pizarrones y pizarrones con fórmulas matemáticas escribió la expresión del teorema de Fermat. "Creo que me detendré aquí", concluyó. Todos los asistentes se pusieron de pie y aplaudieron. La noticia de la demostración del Último Teorema de Fermat llegó a los medios y apareció en la primera página del New York Times, algo poco habitual para la noticia de la demostración de un teorema. Además, Wiles fue incluido entre las personas más influyentes del año por la revista People.
Sin embargo, antes de declararse demostrado el teorema, el trabajo de Wiles tenía que ser revisado por otros matemáticos. Después de todo, la demostración podía estar equivocada. Y, efectivamente, lo estaba. En algún punto de la demostración, Wiles había cometido un error. Entonces volvió al trabajo y el 25 de octubre de 1994 presentó una demostración revisada. Esta vez no hubo errores y la demostración fue publicada en la edición de mayo de 1995 de los Anales de Matemáticas de la Universidad de Princeton. Cinco meses después se emitió el episodio de Los Simpson con el homenaje más original a la noticia matemática más importante del siglo XX.
(*) Docente y divulgador científico.















Dejanos tu comentario
Los comentarios realizados son de exclusiva responsabilidad de sus autores y las consecuencias derivadas de ellos pueden ser pasibles de las sanciones legales que correspondan. Evitar comentarios ofensivos o que no respondan al tema abordado en la información.